Abhiraj Singh - Robotics Engineer & Software Developer

Introduction to Exoskeleton Control Strategies

Powered lower-body exoskeletons have revolutionized mobility solutions for individuals with lower limb disabilities. While commercial exoskeletons like Atalante by Wandercraft and xoMotion employ various control strategies, Model Predictive Control (MPC) has emerged as a powerful approach for trajectory generation and control. This study presents an advanced MPC framework specifically designed for offline trajectory generation in powered lower-body exoskeletons, with particular focus on the WalkOn F1 exoskeleton developed at the Korea Advanced Institute of Science and Technology (KAIST).

The WalkOn F1 exoskeleton represents a significant advancement in assistive robotics, designed to provide enhanced mobility for individuals with lower-limb impairments. Developed at KAIST's Exolab Laboratory, this exoskeleton features a sophisticated mechanical design with 12 degrees of freedom and advanced actuation systems. The development of an effective control strategy for the WalkOn F1 presented unique challenges due to its complex dynamics and the need for precise motion control.

This work specifically addresses the challenge of offline trajectory generation for the WalkOn F1 exoskeleton, which is crucial for:

Planning stable and efficient walking patterns
Optimizing energy consumption during operation
Ensuring smooth transitions between different motion phases
Maintaining dynamic balance throughout the gait cycle
Adapting to various walking scenarios and user requirements

The MPC framework developed in this study provides a systematic approach to generating optimal trajectories that satisfy these requirements while considering the exoskeleton's physical constraints and dynamic capabilities. By focusing on offline trajectory generation, we can ensure the safety and reliability of the planned motions before their execution, which is particularly important for users with mobility impairments.

Comparison with Commercial Exoskeletons

Atalante by Wandercraft

Atalante utilizes a full dynamic walking model with self-balancing control, featuring:

Model Predictive Control (MPC) for real-time trajectory optimization
Real-time dynamic balance control through MPC-based state estimation
Advanced algorithms for adaptive gait generation and prediction
Sensor feedback integration for responsive movements
Multi-directional locomotion capabilities
FDA-approved for rehabilitation settings

xoMotion Exoskeleton

xoMotion employs a hybrid control approach combining MPC with machine learning:

Model Predictive Control for trajectory planning and optimization
Dynamic balance control with real-time adaptation through MPC
Continuous learning from user movements for MPC parameter tuning
Integration of user feedback for personalized assistance
Support for various walking tasks with MPC-based motion planning
Full autonomy for complex movements using predictive control

MPC-Based Control Advantages

The MPC framework developed in this study offers several advantages over traditional control methods:

Predictive capability for robust trajectory generation
Explicit handling of system constraints
Optimal performance through cost function minimization
Offline trajectory generation for precise motion planning
Comprehensive state estimation and sensor fusion

This post focuses on developing an MPC-based control strategy that can generate optimal trajectories for powered lower-body exoskeletons, with particular emphasis on stability, efficiency, and adaptability to different user needs and environmental conditions.

1. System Modeling

State-Space Model

The state of a multibody system is described by:

x = [q \dot{q}]

where $q$ are generalized coordinates and $\dot{q}$ are velocities.

System Architecture and Sensors

Figure: WalkOn-F1 exoskeleton system architecture. The exoskeleton features 12 actuated joints (6 degrees of freedom per leg), including hip, knee, and ankle joints. Key sensors for feedback include joint angle encoders, an IMU for trunk orientation, and foot sensors for Center of Pressure (CoP) and Ground Reaction Force (GRF) data. This hardware configuration provides the necessary state informations: joint positions, velocities, and external forces, used in the state-space model and system modeling described in this section.

Implementation:

Python

script.py

self.actuation = crocoddyl.ActuationModelFloatingBase(self.state)

Algorithmic Context: Robot Model Initialization

The robot model initialization involves setting up the exoskeleton's kinematic and dynamic properties, which are essential for accurately simulating its behavior. This includes defining the model's joints, links, and actuation mechanisms.

Mathematically, the robot model can be represented by:

q = [q_{base}, q_{joints}]^{⊤}

\dot{q} = [\dot{q}_{base}, \dot{q}_{joints}]^{⊤}

Where:

$q \in R^{n_{q}}$ is the vector of generalized coordinates, consisting of the base position and orientation ( $q_{base} \in R^{7}$ ) and the joint angles ( $q_{joints} \in R^{n_{j}}$ ).
$\dot{q} \in R^{n_{v}}$ is the vector of generalized velocities, consisting of the base linear and angular velocities ( $\dot{q}_{base} \in R^{6}$ ) and the joint velocities ( $\dot{q}_{joints} \in R^{n_{j}}$ ).
$n_{q}$ is the total number of generalized coordinates, $n_{v}$ is the total number of generalized velocities, and $n_{j}$ is the number of actuated joints.

Python

script.py

class GaitControlMPC:
    def __init__(self, rmodel, rightFoot, leftFoot, integrator="euler", control="zero", 
            fwddyn=True, firstStep=False):
        self.rmodel = rmodel
        self.rdata = rmodel.createData()
        self.state = crocoddyl.StateMultibody(self.rmodel)
        self.actuation = crocoddyl.ActuationModelFloatingBase(self.state)
        self.rfId = self.rmodel.getFrameId(rightFoot)
        self.lfId = self.rmodel.getFrameId(leftFoot)
        self._integrator = integrator
        self._control = control
        self._fwddyn = fwddyn
        q0 = np.zeros(self.rmodel.nq)
        self.rmodel.defaultState = np.concatenate([q0, np.zeros(self.rmodel.nv)])
        self.mu = 0.3
        self.Rsurf = np.eye(3)
        self.footBox = np.array([0.32, 0.17]) * 0.25
        self.comInitialHeight = pin.centerOfMass(self.rmodel, self.rdata, q0)[2]

Equations of Motion

M (q) \ddot{q} + C (q, \dot{q}) \dot{q} + g (q) = u

$M$ : mass/inertia matrix
$C$ : Coriolis/centrifugal
$g$ : gravity
$u$ : control inputs

Implementation:

Python

script.py

# Mass matrix
pin.crba(self.rmodel, self.rdata, q)
# Coriolis
pin.computeCoriolisMatrix(self.rmodel, self.rdata, q, q_dot)
# Gravity
pin.computeGeneralizedGravity(self.rmodel, self.rdata, q)

Discrete-Time State-Space Update

x_{k + 1} = f (x_{k}, u_{k})

q_{k + 1} = q_{k} + Δ t \dot{q}_{k}

\dot{q}_{k + 1} = \dot{q}_{k} + Δ t \ddot{q}_{k}

Initial State and Control Input

The initial state vector $x_{0}$ includes the initial positions and velocities of the exoskeleton's joints and links:

x_{0} = [q_{0} \dot{q}_{0}]

Where:

$q_{0} \in R^{n_{q}}$ is the initial generalized coordinates.
$\dot{q}_{0} \in R^{n_{v}}$ is the initial generalized velocities.

The initial control input vector $u_{0}$ represents the initial torques or forces applied to the exoskeleton's joints and floating base:

u_{0} = [τ_{base} τ_{joints}]

Where:

$τ_{base} \in R^{6}$ represents the forces and torques applied to the floating base.
$τ_{joints} \in R^{n_{j}}$ represents the torques applied to the actuated joints.

Python

script.py

class GaitController:
    def __init__(self, WPGmodel: GaitControlMPC, robot, rightFoot, leftFoot, display):
        self.robot = robot
        self.rightFoot = rightFoot
        self.leftFoot = leftFoot
        self.display = display
        self.WPG = WPGmodel
        self.knotScaler = 1
        self.timeStep = 0.01
        self.initialize()

    def initialize(self):
        self.gait = self.WPG(self.robot.model, self.rightFoot, self.leftFoot)
        self.gait.RL_StairN = np.array([0, 0])
        q0 = self.robot.q0.copy()
        v0 = pin.utils.zero(self.robot.model.nv)
        self.x0 = np.concatenate([q0, v0])
        self.x_last = self.x0
        self.xs = np.array([self.x_last])
        self.xs_hist = np.array([])
        self.us_hist = np.array([])

Algorithmic Context: State Prediction in the MPC Loop

State prediction is the first step in the MPC loop, where the future states of the exoskeleton are estimated based on the current state and control inputs. This prediction forms the basis for the optimization problem that follows.

The predicted state $x_{k + 1}$ at time step $k + 1$ is obtained using the system dynamics model:

x_{k + 1} = f (x_{k}, u_{k})

where:

$x_{k} \in R^{n_{x}}$ is the state vector at time step $k$ ,
$u_{k} \in R^{n_{u}}$ is the control input vector at time step $k$ ,
$f$ represents the system dynamics function, incorporating both kinematic and dynamic models of the exoskeleton.

In the provided code, state prediction is handled within the Crocoddyl framework using the differential action models defined for various phases of the exoskeleton's motion. The key component for state prediction is the forward dynamics integration, which updates the state based on the current control input. This estimated state is then used as the starting point for the MPC optimization at each control cycle.

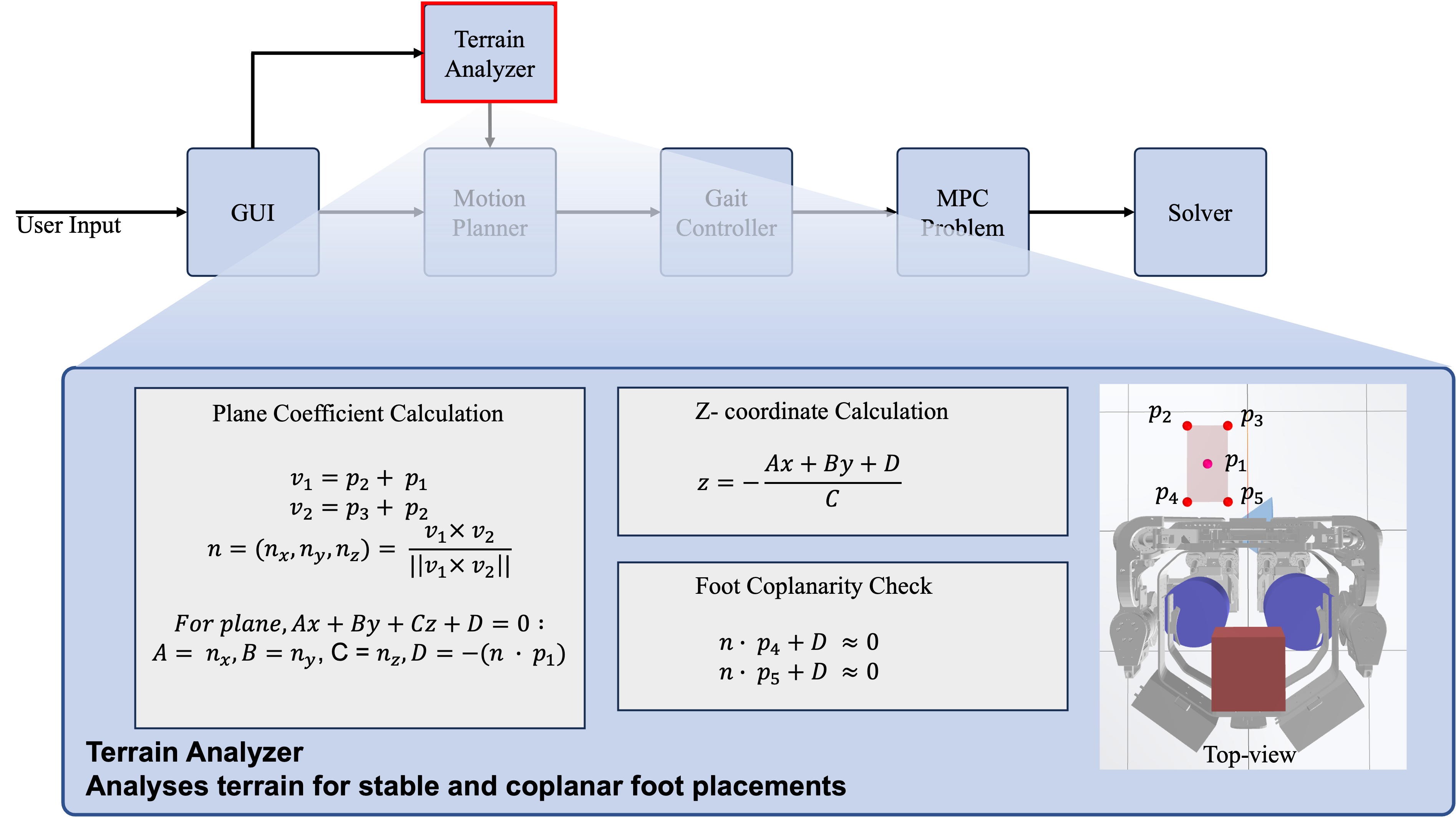
Terrain Analyzer for Step Planning

Figure: The Terrain Analyzer module evaluates the safety and feasibility of each next step before execution. It analyzes the terrain to ensure stable and coplanar foot placements, calculates the supporting plane coefficients, and determines the height of the next step. This process is essential for robust and adaptive exoskeleton walking, as it prevents unsafe steps and enables the exoskeleton to adapt to uneven or changing surfaces.

3. Constraints

State Constraints

x_{m i n} \leq x_{k} \leq x_{m a x}

Implementation:

Python

script.py

xlb = np.concatenate([...])
xub = np.concatenate([...])
bounds = crocoddyl.ActivationBounds(xlb, xub, 1.0)
xLimitResidual = crocoddyl.ResidualModelState(self.state, np.zeros_like(x0), nu)
xLimitActivation = crocoddyl.ActivationModelQuadraticBarrier(bounds)
limitCost = crocoddyl.CostModelResidual(self.state, xLimitActivation, xLimitResidual)
costModel.addCost("xLimit", limitCost, 1e10)

Control Input Constraints

u_{m i n} \leq u_{k} \leq u_{m a x}

Implementation:

Python

script.py

ctrlResidual = crocoddyl.ResidualModelControl(self.state, nu)
ctrlReg = crocoddyl.CostModelResidual(self.state, ctrlResidual)
costModel.addCost("ctrlReg", ctrlReg, 1e2)

Contact Constraints (Friction Cone)

f_{contact} \in K_{friction} (μ) = {f ∣ ∥ f_{tangential} ∥ \leq μ f_{normal}}

Implementation:

Python

script.py

cone = crocoddyl.WrenchCone(self.Rsurf, self.mu, self.footBox)
wrenchResidual = crocoddyl.ResidualModelContactWrenchCone(self.state, i, cone, nu, self._fwddyn)
wrenchActivation = crocoddyl.ActivationModelQuadraticBarrier(crocoddyl.ActivationBounds(cone.lb, cone.ub))
wrenchCone = crocoddyl.CostModelResidual(self.state, wrenchActivation, wrenchResidual)
costModel.addCost(self.rmodel.frames[i].name + "_wrenchCone", wrenchCone, 1e4)

Algorithmic Context: Constraint Handling in the MPC Loop

Constraint handling ensures that the exoskeleton's motion adheres to physical and operational limits, such as joint position and velocity bounds, contact force limits, and obstacle avoidance.

The constraints can be expressed as:

x_{min} \leq x_{k} \leq x_{max} u_{min} \leq u_{k} \leq u_{max} g (x_{k}, u_{k}) \leq 0

where:

$x_{min}, x_{max} \in R^{n_{x}}$ are the state bounds,
$u_{min}, u_{max} \in R^{n_{u}}$ are the control input bounds,
$g (x_{k}, u_{k})$ represents other constraint functions, such as contact stability.

In the code, constraints are integrated into the optimization problem using Crocoddyl's activation and residual models. For example, joint limits and velocity bounds are handled by setting up quadratic barrier costs, while contact forces are managed using wrench cone constraints. These constraints are enforced at each time step within the prediction horizon, ensuring that the generated motion is both feasible and safe for the exoskeleton and its user.

4. Cost Function

Quadratic Cost Formulation

J = k = 0 \sum N - 1 ((x_{k} - x_{ref, k})^{⊤} Q (x_{k} - x_{ref, k}) + u_{k}^{⊤} R u_{k}) + (x_{N} - x_{ref, N})^{⊤} Q_{N} (x_{N} - ref, N)

State deviation penalty: $Q$
Control effort penalty: $R$
Terminal state penalty: $Q_{N}$

Implementation:

Python

script.py

stateResidual = crocoddyl.ResidualModelState(self.state, self.rmodel.defaultState, nu)
stateActivation = crocoddyl.ActivationModelWeightedQuad(stateWeights**2)
stateReg = crocoddyl.CostModelResidual(self.state, stateActivation, stateResidual)

ctrlResidual = crocoddyl.ResidualModelControl(self.state, nu)
ctrlReg = crocoddyl.CostModelResidual(self.state, ctrlResidual)

costModel.addCost("stateReg", stateReg, 1e1)
costModel.addCost("ctrlReg", ctrlReg, 1e2)

Algorithmic Context: Cost Calculation in the MPC Loop

The cost calculation step involves evaluating the cost function for the predicted states and control inputs. The cost function quantifies the performance of the exoskeleton's control strategy, penalizing deviations from the desired trajectory, excessive control inputs, and violations of constraints.

The cost function $J$ at time step $k$ can be expressed as:

J_{k} = i = k \sum k + N - 1 (x_{i}^{T} Q x_{i} + u_{i}^{T} R u_{i}) + x_{k + N}^{T} Q_{N} x_{k + N}

where:

$Q \in R^{n_{x} \times n_{x}}$ is the state weighting matrix,
$R \in R^{n_{u} \times n_{u}}$ is the control input weighting matrix,
$Q_{N} \in R^{n_{x} \times n_{x}}$ is the terminal state weighting matrix,
$N$ is the prediction horizon.

The provided code defines various cost models using Crocoddyl's 'CostModelSum' class, which aggregates different cost components such as state regularization, control regularization, and task-specific costs like foot trajectory tracking and center of mass (CoM) positioning. These cost models are then used by the optimization solver to evaluate and minimize the total cost over the prediction horizon, ensuring that the exoskeleton follows the desired trajectory while minimizing control effort and respecting constraints.

5. Contact and Friction Models

Contact Model

f_{contact} = [f_{trans} m_{rot}]

Implementation:

Python

script.py

contactModel = crocoddyl.ContactModelMultiple(self.state, nu)
supportContactModel = crocoddyl.ContactModel6D(
    self.state, i, pin.SE3.Identity(), pin.LOCAL_WORLD_ALIGNED, nu, np.array([0.0, 50.0]),
)
contactModel.addContact(self.rmodel.frames[i].name + "_contact", supportContactModel)

6. Trajectory Planning

Prediction Horizon and Gait Phases

Prediction horizon: $N$ time steps, each of duration $Δ t$
Phases: Double support, before swing, swing, zero velocity

N = (t_{1} \times supportKnots) + (t_{2} \times stepKnots)

Implementation:

Python

script.py

doubleSupport = [self.createSwingFootModel(x0, timeStep, [self.rfId, self.lfId], RL_StairN=self.RL_StairN) for k in range(int(supportKnots*0.4))]
swingStepModels = self.createFootstepModels(...)
loco3dModel = doubleSupport + beforeSwing + swingStepModels + doubleSupport + doubleSupportZeroVel
problem = crocoddyl.ShootingProblem(x0, loco3dModel[:-1], loco3dModel[-1])

Algorithmic Context: Main MPC Loop

The main loop of the Model Predictive Control (MPC) algorithm involves the continuous repetition of several key steps: state prediction, cost calculation, constraint handling, and optimization solver integration. This loop ensures that the exoskeleton's control inputs are updated in real-time, enabling it to follow the desired trajectory while adhering to the system's constraints.

Pseudo Code:

Python

script.py

for t in range(timesteps):
    # Predict future states
    state_prediction()
    
    # Calculate cost for predicted states and control inputs
    cost_calculation()
    
    # Handle constraints
    constraint_handling()
    
    # Solve the optimization problem
    solver.solve(init_xs, init_us, maxiter, False, regInit)
    
    # Update state and control inputs
    update_state_and_control()

Algorithmic Context: Walking Problem Generation

The MPC framework supports various walking scenarios, such as flat walk, terrain walk, rotation, and custom walk. Each scenario involves a specific sequence of kinematic and dynamic steps to generate the appropriate walking problem for the optimizer.

Flat Walk Problem Pseudo Code:

Python

script.py

Algorithm CreateFlatWalkProblem(x0, step_x, step_y, stepHeight, timeStep, 
    stepKnots, supportKnots, taskSwingFoot, firstStep, doubleGen):
    Initialize rmodel, rdata, state, actuation
    Initialize frame IDs for rightFoot, leftFoot
    
    Call forwardKinematics(rmodel, rdata, x0[:state.nq])
    Call updateFramePlacements(rmodel, rdata)
    
    if taskSwingFoot == "right":
        taskSupportFootId = lfId
        taskSwingFootId = rfId
    else if taskSwingFoot == "left":
        taskSupportFootId = rfId
        taskSwingFootId = lfId
    
    oRsupport = rdata.oMf[taskSupportFootId].rotation
    oMsupport = rdata.oMf[taskSupportFootId]
    
    Define stepSE3 as Identity SE3
    stepSE3.rotation = oRsupport
    stepSE3.translation = oMsupport * [step_x, step_y, 0.0]
    stepSE3.translation[2] = 0.0
    
    problem = CreateSwingFromSE3(x0, stepSE3, stepHeight, timeStep, stepKnots, 
                supportKnots, taskSwingFoot, firstStep, doubleGen)
    return problem

Terrain Walk Problem Pseudo Code:

Python

script.py

Algorithm CreateTerrainWalkProblem(x0, step_x, step_y, stepHeight, timeStep, 
        stepKnots, supportKnots, taskSwingFoot, firstStep, 
        doubleGen, 
        terrainNormal, terrainMidZ):
    Initialize rmodel, rdata, state, actuation
    Initialize frame IDs for rightFoot, leftFoot
    
    Call forwardKinematics(rmodel, rdata, x0[:state.nq])
    Call updateFramePlacements(rmodel, rdata)
    
    if taskSwingFoot == "right":
        taskSupportFootId = lfId
        taskSwingFootId = rfId
    else if taskSwingFoot == "left":
        taskSupportFootId = rfId
        taskSwingFootId = lfId
    
    oRsupport = rdata.oMf[taskSupportFootId].rotation
    oMsupport = rdata.oMf[taskSupportFootId]
    
    Define stepSE3 as Identity SE3
    stepSE3.rotation = GetNewFootOrientation(oRsupport, terrainNormal)
    stepSE3.translation = oMsupport * [step_x, step_y, 0.0]
    stepSE3.translation[2] = terrainMidZ
    
    problem = CreateSwingFromSE3(x0, stepSE3, stepHeight, timeStep, stepKnots, 
        supportKnots, taskSwingFoot, firstStep, doubleGen, terrain="uneven")
    return problem

Function GetNewFootOrientation(R_foot, n):
    Normalize n
    zw_foot_new = n
    xw_foot_new = Project xw_foot onto the plane defined by n and normalize
    yw_foot_new = Cross product of n and xw_foot_new
    R_foot_new = Construct rotation matrix from xw_foot_new, yw_foot_new, zw_foot_new
    return R_foot_new

Rotation Problem Pseudo Code:

Python

script.py

Algorithm CreateRotationProblem(x0, stepYaw, stepHeight, timeStep, stepKnots, 
    supportKnots, taskSwingFoot, firstStep, doubleGen, terrainNormal, terrainMidZ):
    Initialize rmodel, rdata, state, actuation
    Initialize frame IDs for rightFoot, leftFoot
    
    Call forwardKinematics(rmodel, rdata, x0[:state.nq])
    Call updateFramePlacements(rmodel, rdata)
    
    if taskSwingFoot == "right":
        taskSupportFootId = lfId
        taskSwingFootId = rfId
        stepYaw = -deg2rad(stepYaw)
    else if taskSwingFoot == "left":
        taskSupportFootId = rfId
        taskSwingFootId = lfId
        stepYaw = deg2rad(stepYaw)
    
    Calculate new foot position [stepXY, rotYaw] using CalcRotFootPos(stepYaw, taskSwingFoot, 
            rdata.oMf[rfId], rdata.oMf[lfId])
    
    Define footFlatSE3 as Identity SE3
    footFlatSE3.rotation = rpyToMatrix([0, 0, rotYaw]) @ rdata.oMf[taskSwingFootId].rotation
    footFlatSE3.translation[:2] = stepXY
    
    Define footTerrainSE3 as Identity SE3
    footTerrainSE3.rotation = GetNewFootOrientation(footFlatSE3.rotation, terrainNormal)
    footTerrainSE3.translation[:2] = stepXY
    footTerrainSE3.translation[2] = terrainMidZ
    
    problem = CreateSwingFromSE3(x0, footTerrainSE3, stepHeight, timeStep, 
            stepKnots, supportKnots, taskSwingFoot, firstStep, doubleGen)
    return problem

Function CalcRotFootPos(rotYaw, direction, rfSE3, lfSE3):
    Define L as 0.1
    Define rotMat as rotation matrix for rotYaw
    Calculate xy_footRight and xy_footLeft using frame placements
    if direction == "right":
        l_hypo = L/2 * 1/sin(abs(rotYaw/2))
        o_rot = l_HR + l_hypo * (l_HR - l_FR) / norm(l_HR - l_FR)
        o_r_dummy = l_HR + l_FR - xy_footLeft - o_rot
        xy_footRight = rotMat @ o_r_dummy + o_rot
        return [xy_footRight, rotYaw]
    else if direction == "left":
        r_hypo = L/2 * 1/sin(abs(rotYaw/2))
        o_rot = r_HL + r_hypo * (r_HL - r_FL) / norm(r_HL - r_FL)
        o_l_dummy = r_FL + r_HL - xy_footRight - o_rot
        xy_footLeft = rotMat @ o_l_dummy + o_rot
        return [xy_footLeft, rotYaw]

Custom Walk Problem Pseudo Code:

Python

script.py

Algorithm CreateCustomWalkProblem(x0, step_x, step_y, stepHeight, stepYaw, timeStep, 
    stepKnots, supportKnots, taskSwingFoot, firstStep, doubleGen, terrainNormal, terrainMidZ):
    Initialize rmodel, rdata, state, actuation
    Initialize frame IDs for rightFoot, leftFoot
    
    Call forwardKinematics(rmodel, rdata, x0[:state.nq])
    Call updateFramePlacements(rmodel, rdata)
    
    if stepYaw > 90:
        Raise ValueError("stepYaw should be less than 90 degrees")
    
    if taskSwingFoot == "right":
        taskSupportFootId = lfId
        taskSwingFootId = rfId
        stepYaw = -deg2rad(stepYaw)
    else if taskSwingFoot == "left":
        taskSupportFootId = rfId
        taskSwingFootId = lfId
        stepYaw = deg2rad(stepYaw)
    
    Calculate new foot position [stepXY, rotYaw] using CalcRotFootPos(stepYaw, 
        taskSwingFoot, rdata.oMf[rfId], rdata.oMf[lfId])
    
    Define footFlatSE3 as Identity SE3
    footFlatSE3.rotation = rpyToMatrix([0, 0, rotYaw]) @ rdata.oMf[taskSwingFootId].rotation
    footFlatSE3.translation[:2] = stepXY
    
    Define footTerrainSE3 as Identity SE3
    footTerrainSE3.rotation = GetNewFootOrientation(footFlatSE3.rotation, terrainNormal)
    footTerrainSE3.translation[:2] = stepXY
    footTerrainSE3.translation[2] = terrainMidZ
    
    if taskSwingFoot == "right":
        taskSupportFootId = lfId
        step_y = -step_y
    else if taskSwingFoot == "left":
        taskSupportFootId = rfId
    
    oMsupport = rdata.oMf[taskSupportFootId]
    footTerrainSE3.translation = oMsupport * [step_x, step_y, 0.0]
    footTerrainSE3.translation[2] = terrainMidZ
    
    problem = CreateSwingFromSE3(x0, footTerrainSE3, stepHeight, timeStep, 
        stepKnots, supportKnots, taskSwingFoot, firstStep, doubleGen)
    return problem

7. Optimization and Solver

Forward and Inverse Dynamics

Forward dynamics:

M (q) \ddot{q} + h (q, \dot{q}) = S^{⊤} τ + J^{⊤} F_{ext}

Implementation:

Python

script.py

dmodel = crocoddyl.DifferentialActionModelContactFwdDynamics(self.state, self.actuation, contactModel, costModel, 0.0, True)

Inverse dynamics:

τ = M (q) \ddot{q} + h (q, \dot{q}) - J^{⊤} F_{ext}

Implementation:

Python

script.py

dmodel = crocoddyl.DifferentialActionModelContactInvDynamics(self.state, self.actuation, contactModel, costModel)

DDP Solver

Backward Pass:

Q_{k} (δ x_{k}, δ u_{k}) = \frac{1}{2} [δ x_{k} δ u_{k}]^{⊤} [Q_{xx, k} Q_{ux, k} Q_{xu, k} Q_{uu, k}] [δ x_{k} δ u_{k}] + [Q_{x, k} Q_{u, k}]^{⊤} [δ x_{k} δ u_{k}]

Optimal control law:

u_{k}^{*} = u_{k} - Q_{uu, k}^{- 1} (Q_{u, k} + Q_{ux, k} δ x_{k})

Forward Pass:

x_{k + 1} u_{k} = f (x_{k}, u_{k}^{*}) = u_{k}^{*} + K_{k} (x_{k} - x_{k}^{*})

Where $K_{k} = - Q_{uu, k}^{- 1} Q_{ux, k}$ is the feedback gain matrix.

Implementation:

Python

script.py

ddp = crocoddyl.SolverBoxFDDP(problem)
ddp.th_stop = 1e-9
init_xs = [self.x_last] * (problem.T + 1)
init_us = []
maxiter = 10000
regInit = 0.1
feasibility = ddp.solve(init_xs, init_us, maxiter, False, regInit)
if not feasibility:
    raise RuntimeError("The optimal control problem is not feasible")

8. Results, Features, Future Directions, Conclusion

Implementation and Results

The MPC framework was implemented using the following key components:

Dynamic Model: A comprehensive multibody dynamics model of the exoskeleton
Optimization Solver: DDP-based solver for handling nonlinearities
Constraint Management: Barrier functions for state and control constraints
Real-time Implementation: Efficient computation for real-time control

Simulation Results

Below are results from the MPC framework in simulation, demonstrating robust and adaptive walking behaviors in various scenarios:

Normal Walking

Normal walking: The exoskeleton follows a straight walking trajectory, maintaining balance and smooth motion.

Side Walking

Side walking: The exoskeleton performs lateral steps, showcasing the controller's ability to handle non-forward walking.

Stair Climbing

Stair climbing: The exoskeleton successfully ascends stairs, adapting foot placement and height for each step.

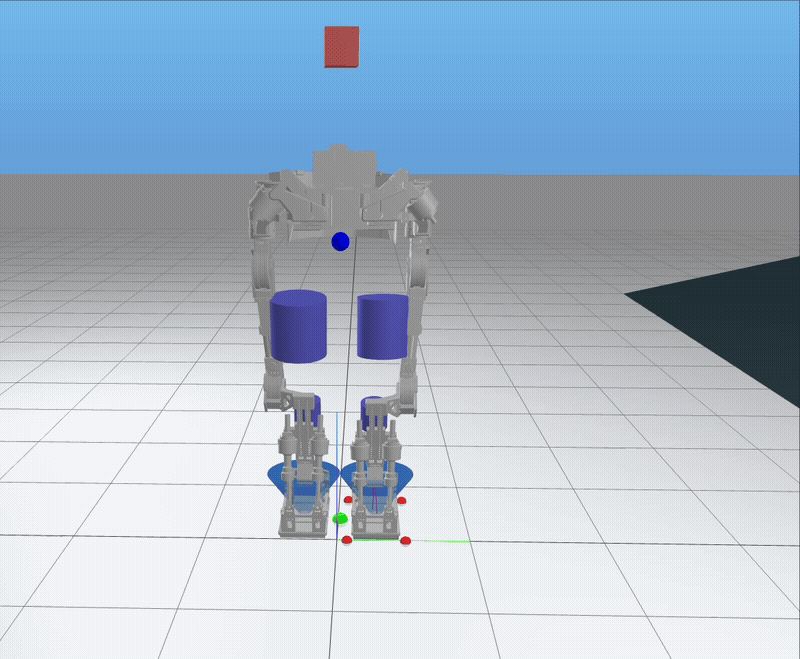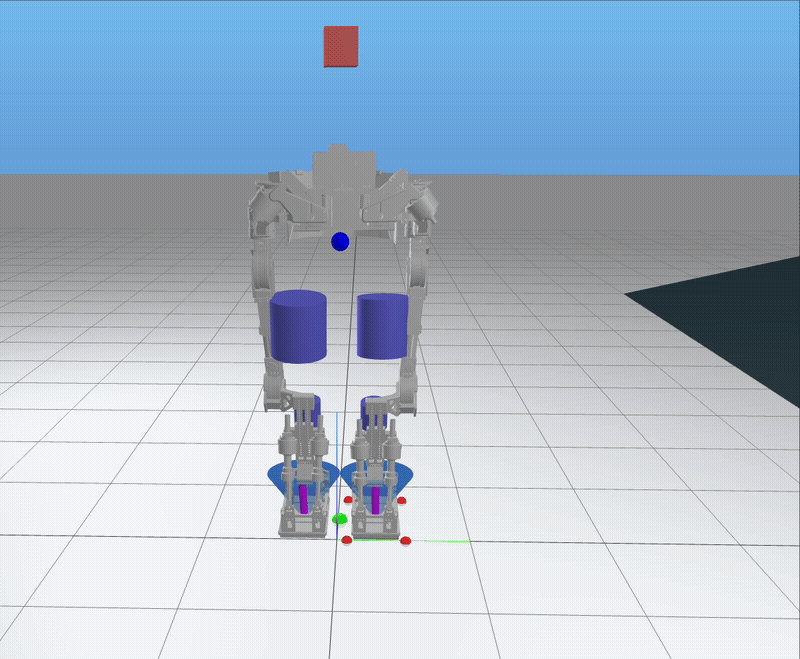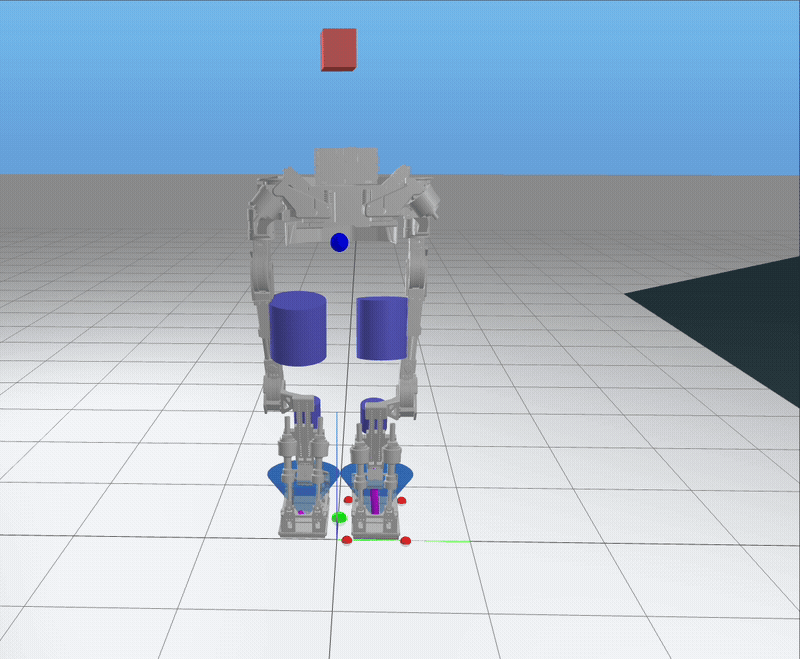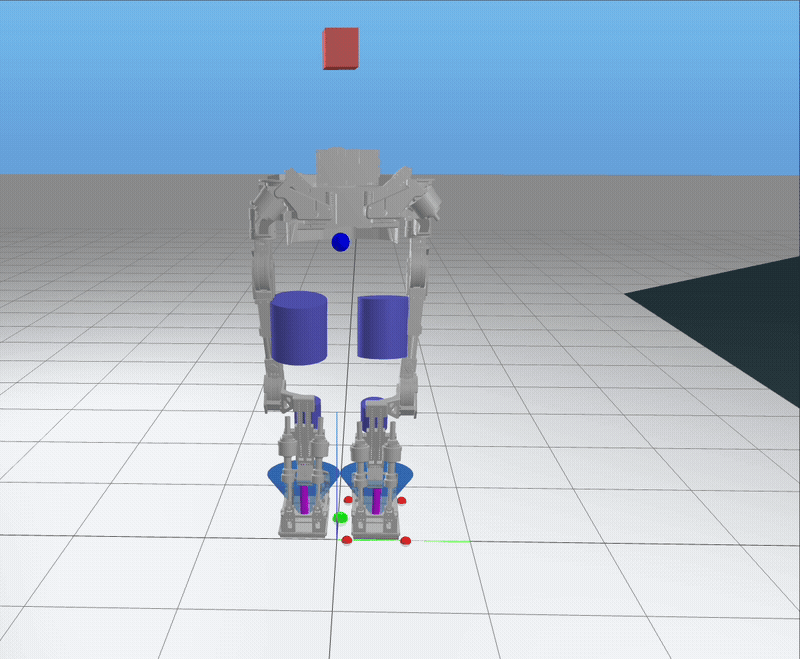
Trotting

Trotting: The exoskeleton executes a dynamic, alternating gait, highlighting the versatility of the MPC approach.

Future Directions

Real-time Optimization: Development of faster optimization algorithms for real-time control
Machine Learning Integration: Incorporation of learning-based methods for enhanced prediction
Complex Terrain Adaptation: Extension to handle diverse operational scenarios
User-Specific Adaptation: Personalization of control parameters based on user characteristics

Conclusion

Model Predictive Control provides a powerful framework for controlling powered lower-body exoskeletons. The combination of predictive capabilities, optimal performance, and explicit constraint handling makes MPC particularly suitable for these complex robotic systems. Future research will focus on improving real-time performance and expanding the range of applications.

This work was conducted at KAIST's ExoLab under the guidance of Prof. Kong.

Model Predictive Control for Powered Lower-Body Exoskeleton Robots

Introduction to Exoskeleton Control Strategies

Comparison with Commercial Exoskeletons

Atalante by Wandercraft

xoMotion Exoskeleton

MPC-Based Control Advantages

1. System Modeling

State-Space Model

Algorithmic Context: Robot Model Initialization

Equations of Motion

Discrete-Time State-Space Update

Initial State and Control Input

Algorithmic Context: State Prediction in the MPC Loop

3. Constraints

State Constraints

Control Input Constraints

Contact Constraints (Friction Cone)

Algorithmic Context: Constraint Handling in the MPC Loop

4. Cost Function

Quadratic Cost Formulation

Algorithmic Context: Cost Calculation in the MPC Loop

5. Contact and Friction Models

Contact Model

6. Trajectory Planning

Prediction Horizon and Gait Phases

Algorithmic Context: Main MPC Loop

Algorithmic Context: Walking Problem Generation

7. Optimization and Solver

Forward and Inverse Dynamics

DDP Solver

8. Results, Features, Future Directions, Conclusion

Implementation and Results

Simulation Results

Future Directions

Conclusion